Statistică - modelul clasic de regresie

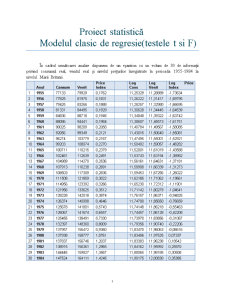
În cadrul următoarei analize dispunem de un eșantion cu un volum de 30 de informații privind consumul real, venitul real și nivelul prețurilor înregistrate în perioada 1955-1984 la nivelul Marii Britanii.

Anul Consum Venit Price Index Log Cons Log Venit Log Price Index

1 1955 77133 79929 0,1762 11,25329 11,28889 -1,73634

2 1956 77825 81975 0,1831 11,26222 11,31417 -1,69795

3 1957 79425 83266 0,1888 11,28257 11,32980 -1,66695

4 1958 81331 84495 0,1929 11,30628 11,34445 -1,64539

5 1959 84836 88718 0,1945 11,34848 11,39322 -1,63742

6 1960 88086 94441 0,1984 11,38607 11,45573 -1,61751

7 1961 90025 98289 0,2058 11,40784 11,49567 -1,58085

8 1962 92056 99349 0,2121 11,43015 11,50640 -1,55081

9 1963 96274 103779 0,2167 11,47495 11,55001 -1,52921

10 1964 99203 108074 0,2270 11,50492 11,59057 -1,48282

11 1965 100711 110215 0,2379 11,52001 11,61019 -1,43588

12 1966 102481 112639 0,2491 11,53743 11,63194 -1,38982

13 1967 104989 114270 0,2536 11,56161 11,64631 -1,37181

14 1968 107913 116238 0,2691 11,58908 11,66339 -1,31273

15 1969 108503 117309 0,2836 11,59453 11,67256 -1,26022

16 1970 111508 121859 0,3022 11,62185 11,71062 -1,19661

17 1971 114956 123392 0,3266 11,65230 11,72312 -1,11901

18 1972 121956 133625 0,3512 11,71142 11,80279 -1,04641

19 1973 128228 142018 0,3874 11,76157 11,86371 -0,94825

20 1974 126374 140998 0,4646 11,74700 11,85650 -0,76659

21 1975 125678 141801 0,5743 11,74148 11,86218 -0,55463

22 1976 126067 141674 0,6557 11,74457 11,86128 -0,42208

23 1977 125455 138491 0,7330 11,73970 11,83856 -0,31067

24 1978 132397 148360 0,8009 11,79356 11,90740 -0,22206

25 1979 137957 156472 0,9360 11,83470 11,96063 -0,06616

26 1980 137938 158777 1,0761 11,83456 11,97525 0,07337

27 1981 137837 156746 1,2037 11,83383 11,96238 0,18542

28 1982 138915 156361 1,2965 11,84162 11,95992 0,25970

29 1983 144445 159827 1,3567 11,88065 11,98185 0,30508

30 1984 147524 164111 1,4245 11,90175 12,00830 0,35385

După cum se poate observa, datele ce prezintă informațiile reale sunt prea mari, lucru care duce la o distribuție asimetrică și, de aceea, acestea au fost logaritmate pentru e le putea folosi în modelul de regresie.

Model 1:

ct- logaritmul valorii consumului pentru perioada t;

yt- logaritmul valorii venitului pentru perioada t;

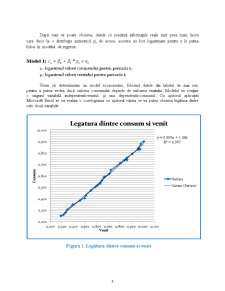
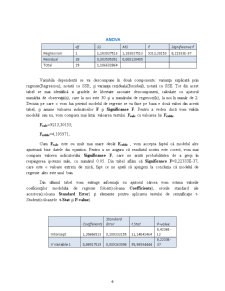
Vrem să detereminăm un model econometric, folosind datele din tabelul de mai sus, pentru a putea vedea dacă valorea consumului depinde de valoarea venitului. Modelul va conține o singură variabilă indepententă-venitul- și una dependentă-consumul. Cu ajutorul aplicației Microsoft Excel se va realiza o corelograma cu ajutorul căreia se va putea observa legătura dintre cele două variabile.

Figura 1. Legătura dintre consum și venit

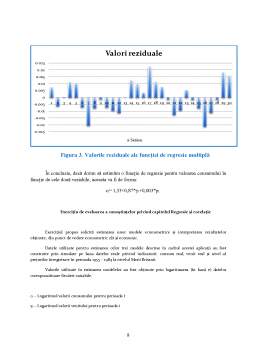
După cum se poate observa în Figura 1, putem spune că între cele două variabile există o legătură directă, punctele fiind grupate în direcția primei bisectoare. În plus, se mai poate observa și că erorile tind să aibă o dispersie constantă. Pentru a estima funcția de regresie care exprimă dependența între cele 2 variabile se va folosi modelul de regresie liniară, tot cu ajutorul aplicației Microsoft Excel.