Distribuția Exponențială

1. Prezentare teoretică

Caracterizare

În teoria probabilităţilor si a statisticii, distribuţia exponenţială, cunoscută şi sub denumirea de distribuţia negativ exponenţială face parte din clasa de distribuţii continue de probabilitate.

Distribuţia exponenţială descrie timpii dintre evenimentele proceselor Poisson, evenimente continue si independente cu o rata medie constantă.

Prin definiţie, distribuţia exponenţială f(x) este:

* f(x) = 0 pentru x < 0

f(x) = λe-λx

* şi pentru x 0 :

Unde este un parametru pozitiv.

Vom arăta că µ din distribuţie este egal cu 1/ şi distribuţia poate fi scrisă:

f(x) = (1/µ).e- x/µ

Proprietăţi:

- Distribuţia exponenţială nu este definită când λ nu este un număr real pozitiv. ( “ExponentialDistribution::posparm: Parameter -1 is expected to be positive.”)

- Substituirea parametrilor invalizi cu rezultate simbolice duce la rezultate lipsite de sens.

- Memorylessness – fiecare eveniment este complet independent de evenimentele anterioare

- Distribuţia exponenţială este un caz special de distribuţie Gamma

2. Aplicaţiile distribuţiei exponentiale în viaţa reală (utilizare)

Distribuţia exponenţială este folosită in descrierea lungimilor intervalelor in procesele omogene Poisson.

In viaţa reală, se foloseste in stabilirea intervalelor precum:

- Timpul până când o particulă radioactivă se descompune sau timpul dintre click-urile unui contor Geiger;

- Timpul până la urmatorul apel telefonic;

- Timpul până când riscul creditarilor se reduce implicit (rambursare credite);

De asemenea, distribuţia exponenţială joacă un rol important in problemele care folosesc conceptul de “lifetime”.

3. Aplicaţii în Mathematica:

Media

Input: Mean[ExponentialDistribution[]]

Output: 1/

Dispersia

Dispersia unei liste de valori este pătratul abaterii standard, adică media pătratelor abaterilor numerelor de la media lor.

Dispersia unei variabile aleatoare X, notată Var(X), este valoarea aşteptată a diferenţei pătrate dintre variabilă şi valoarea ei aşteptată:

Var(X) = Exp((X – E(X))2).

Dispersia unei variabile aleatoare este pătratul erorii standard (SE) a variabilei

Input: Variance[ExponentialDistribution[]]

Output: 1/

Funcţia densităţii de probabilitate

Pentru o variabilă aleatoare continuă, numim densitate de probabilitate acea funcţie (dacă există), f, astfel încât funcţia de repartiţie se poate calcula rezolvand integrala:

Funcţia densităţii de probabilitate permite calculul probabilităţii ca variabilă aleatoare să aparţină unui interval:

P(a<= X <=b) = (aria de sub graficul lui f limitată de a şi b), unde a <= b,

Input: PDF[ExponentialDistribution[],x]

Output:

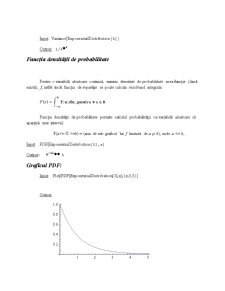
Graficul PDF:

Input: Plot[PDF[ExponentialDistribution[1],x],{x,0,5}]