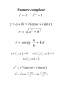Modele de Gestiune a Stocurilor

Extras din referat Cum descarc?

In cadrul proceselor economice, teoria stocurilor a aparut din necesitatea asigurarii unei aprovizionari ritmice si cu cheltuieli minime a stocurilor de materii prime si materiale in procesul de productie sau a stocurilor de produse finite si bunuri de larg consum in activitatea de desfacere a marfurilor. Stocul este ,,o rezerva de bunuri materiale care este creata la unitati economice si care urmeaza a fi consumata, utilizata, in perioada urmatoare sau valorificata ulterior, prin vanzare" .
In vederea optimizarii stocurilor de materii prime si materiale se poate face apel la modele matematice in masura sa gaseasca o solutie matematica care sa conduca la obtinerea raspunsului pentru urmatoarele doua chestiuni:
- determinarea marimii optime a comenzii de aprovizionare;
- determinarea momentului (sau frecventei) optime de aprovizionare.
Unul din cele mai cunoscute modele matematice de determinare a optimului de stocaj este modelul Wilson aplicabil in cazul cererii constante si a unei perioade fixe de aprovizionare, fara posibilitatea aparitiei rupturii de stoc.
Acest model este caracterizat prin:
- perioada de aprovizionare T fixa, deci aprovizionarea se face la intervale egale de timp;
- cerere u constanta in timp, adica pe fiecare perioada de aprovizionare avem aceeasi cerere sau cereri egale pe intervale egale de timp;
- u=v, adica aprovizionarea se face cu cantitatea ceruta;
- aprovizionarea se face in momentul in care stocul devine 0 (nu se admit intervale de timp pe care stocul sa fie 0) si aprovizionarea se face instantaneu (durata dintre momentul lansarii comenzii si intrarea marfurilor in depozit este 0) .
La acest model sunt cunoscute urmatoarele elemente:
- V = cererea totala pe perioada ?;
- ? = perioada de timp pe care se studiaza stocarea;
- Cl = cheltuielile de lansare ale unei comenzi;
- cs = costul unitar de stocare (costul stocarii unei unitati de marfa pe o unitate de timp);
Se urmareste determinarea urmatoarelor variabile care sunt considerate necunoscute :
- u, v (u = v) - cantitatea optima cu care sa se faca aprovizionarea;
- T - durata optima de timp intre doua aprovizionari;
- n - numarul optim de aprovizionari;
- CT - cheltuielile totale legate de gestiunea stocului pe o perioada T de aprovizionare.
Obiectivul modelului este gasirea acestor valori astfel incat C?, cheltuielile totale legate de gestiunea stocului pe o perioada ? sa fie minime.
Pe o perioada de aprovizionare T avem doua categorii de cheltuieli:
- de lansare Cl;
- de stocare, care se exprima prin (pe o perioada T nivelul mediu al stocului este v/2.
Astfel cheltuielile totale legate de gestiunea stocului pe o perioada T pot fi exprimate in urmatorul mod:
CT = Cl + cs T.
Avand n perioade de aprovizionare, rezulta ca C? = n?CT. Inlocuind in relatia de mai sus se obtine:
C? = n? Cl + cs T?n.
Numarul optim de aprovizionari n se poate scrie ca:
n = = = C? = Cl + cs ?.
Cantitatea optima cu care sa se faca aprovizionarea v devine singura necunoscuta. Variabila trebuie determinata astfel incat C? sa fie minime. In acest scop vor fi folosite metodele de determinare a punctelor de extrem. Primul pas este calculul derivatei costului total, rezolvand ecuatia f?(v) = 0, adica - + cs?? = 0 vo = .
Calculand f??(v) = > 0 rezulta ca avem un punct de minim. 
Astfel vo = v = u = ;
n = ;
T = ;
CT = Cl +cs? ? T .
Astfel C? = f = f(v ) = = cs? v ??.
Modelul matematic de optimizare a stocului s-a fundamentat pe un caz particular de aprovizionare potrivit caruia intervalele intre aprovizionari sunt considerate constante, prin urmare aprovizionarea se desfasoara ritmic, iar stocurile se constituie instantaneu si se dau treptat in consum pana la epuizarea totala.

Fisiere in arhiva (1):

 Modele de Gestiune a Stocurilor.doc