Metode de Investigare a Stabilitatii unei Solutii

Extras din referat Cum descarc?

METODA VALORILOR PROPRII
Teoria stabilitatii studiaza proprietatile solutiilor stabile, ofera criterii, care permit pentru ecuatia diferentiala ori sistemul dat si solutia indicata sa conchidem daca este stabila sau nu aceasta solutie. 
Teoria stabilitatii este o ramura importanta a teoriei ecuatiilor diferentiale si joaca un rol important in mecanica si tehnica. Ea a fost creata prin efortul a mai multor matematicieni si fizicieni: A.M. Liapunov, A.Poincare, I.Bendixon si altii. Problema despre stabilitatea miscarii a fost pusa in modul cel mai serios de savantul rus A.M.Liapunov, care a obtinut rezultate fundamentale in teoria stabilitatii, metode stricte de stabilitate si nestabilitate a miscarii. Cercetarile lui A.M.Liapunov au fost continuate cu succes de catre alti matematicieni.
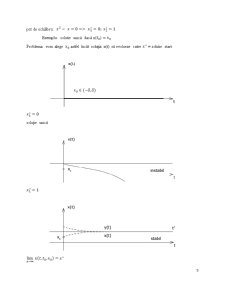
O modalitate buna de a incepe analiza sistemului neliniar 
(1)
este de a determina punctele de echilibru ale (1) si de a descrie comportamentul sistemului (1) langa punctele de echilibru. In urmatoarele sectiuni vom arata comportamentul local al sistemului neliniar (1) langa un punct de echilibru hiperbolic. X0 este calitativ determinat de comportamentul sistemului neliniar
(2) 
cu matricea A = Df(x0) langa origine. Functia liniara Ax=Df(x0) se numeste partea liniara a lui f la x0.
Definitie: Un punct x0 R se numeste punct de echilibru sau punct critic al (1) daca f(x0)=0. Un punct de echilibru x0 este numit punct de echilibru hiperbolic al (1) daca niciuna din valorile proprii ale matricii Df(x0) nu au o parte reala. 
Sistemul liniar (2) cu matricea A = Df(x0) se numeste liniarizarea lui (1) la x0.
Daca x0=0 este punct de echilibru al (1) atunci f(0)=0 si din teorema lui Taylor
Rezulta ca functia liniara Df(0)x constituie o buna aproximare la functia neliniara f(x) langa x(0) si este rezonabil sa ne asteptam ca comportamentul sistemului neliniar (1) langa punctul x0 va fi aproximat de comportamentul neliniar la x=0.
Notam ca daca x0 este un punct de echilibru al (1) si este fluxul ecuatiei diferentiale al (1) atunci ( x0)= x0 pentru toate t R. Astfel, x se numeste punct fix al ; este de asemenea numit un zero, un punct critic sau un punct singular al campului de vectori f: R .

Fisiere in arhiva (1):

 Metode de Investigare a Stabilitatii unei Solutii.doc