Oglinzi 2 Oglinzi plane 3 Oglinzi sferice 3 Oglinzi parabolice 5 Lentilele 5 Lentilele sferice 5 Lentilele cilindrice 9 Lentile torice 10 Lentilele Fresnel 10 Dioptrul sferic 11
Oglinzi Oglinzile sunt elemente optice cu suprafete metalizate care au proprietatea de a reflecta lumina. In functie de forma suprafetelor reflectatoare exista mai multe tipuri de oglinzi: plane, sferice, parabolice. Oglinzi plane Oglinda plana este un sistem acromat cu distanta focala infinita care are proprietatea de stigmatism. Imaginea data de o oglinda plana este dreapta, egala cu obiectul si simetrica fata de suprafata p2 = -p1. Suprafata reflectatoare se obtine prin depuneri metalice, argint, nichel, aluminiu, pe placi de sticla. Exista doua tipuri de oglinzi plane: oglinzi pentru care se metalizeaza suprafata anterioara a lamei si oglinzi pentru care se metalizeaza suprafata posterioara. Oglinzile cu suprafata reflectanta anterioara dau o imagine simetrica a obiectului in raport cu suprafata oglinzii. La o deplasare a oglinzii cu ?p ii corespunde o deplasare a imaginii cu o distanta 2?p. O rotire a oglinzii cu unghiul ?produce o rotire a razei reflectate cu unghiul 2?. In cazul oglinzilor cu suprafata reflectatoare posterioara, pentru protectia stratului de metal se foloseste o lama de sticla cu fete plan paralele. Raza de lumina sufera doua refractii si o reflexie pe suprafata metalizata. Sistemul lama - suprafata metalizata se comporta ca si cum oglinda ar fi fost deplasata cu distanta ?d: ?d=d[1 - cos i(n2 - sin2i)-1/2] unde d este grosimea lamei iar i este unghiul de incidenta pe suprafata lamei. Acest fenomen nu influenteaza comportarea oglinzii. Inconvenientul pe care il prezinta aceste oglinzi este legat de posibilitatea existentei unor reflexii multiple in interiorul lamei de sticla, datorita carora apar mai multe imagini ale obiectului. Oglinzi sferice Oglinzile sferice sunt dioptrii sferici avand o suprafata reflectatoare. Din acest motiv, relatia intre punctele conjugate ( obiect si imagine) pentru o oglinda sferica in domeniul paraxial se obtine punand conditia n' = - n in formula fundamentala a dioptrului sferic. 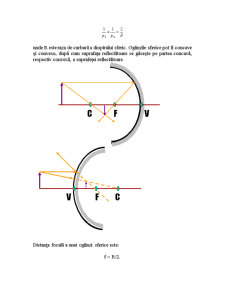Se obtine relatia: unde R este raza de curbura a dioptrului sferic. Oglinzile sferice pot fi concave si convexe, dupa cum suprafata reflectatoare se gaseste pe partea concava, respectiv convexa, a suprafetei reflectatoare. Distanta focala a unei oglinzi sferice este: f = R/2. Oglinzile sferice nu sunt sisteme stigmatice. Un stigmatism aproximativ se poate realiza doar in domeniul razelor paraxiale, raze care prezinta inclinari foarte mici in raport cu axa optica. In conditii obisnuite oglinzile sferice prezinta aberatii geometrice datorita carora imaginea este distorsionata. Oglinzi parabolice Aceste oglinzi au sectiunea de forma unei parabole. Oglinzile parabolice prezinta stigmatism pentru fasciculele paralele de lumina, imaginea formandu-se in acest caz in focarul obiect al oglinzii. Aceste oglinzi au insa dezavantajul unui astigmatism mare si a prezentei altor aberatii cum ar fi coma si curbura campului. Utilizarea oglinzilor in constructia aparatelor optice este avantajoasa datorita faptului ca in acest caz nu apar aberatii cromatice.
După plată vei primi prin email un cod de download pentru a descărca gratis oricare alt referat de pe site.Vezi detalii.
