Cuprins
- GRAFURI NEORIENTATE – NO}IUNI DE BAZ| 1
- GRADE {I {IRURI GRAFICE 3
- CLASE SPECIALE DE GRAFURI 4
- REPREZENTAREA GRAFURILOR NEORIENTATE 6
- PARCURGEREA GRAFURILOR NEORIENTATE 9
- METODA BF 10
- METODA DF 13
- PARCURGERE BF RECURSIV 16
- PARCURGERE DF RECURSIV 18
- BIBLIOGRAFIE 19
- CUPRINS 20
Extras din referat
GRAFURI NEORIENTATE
NOTIUNI INTRODUCTIVE
NOTIUNI DE BAZA
DEFINITIE: Se numeste graf neorientat o pereche ordonata de multimi(X,U), X fiind o multime finita si nevida de elemente numite noduri sau varfuri, iar U o multime de perechi neordonate (submultimi cu doua elemente) din X, numite muchii.
Vom nota cu G=(X,U) un graf neorientat. Multimea X se numeste multimea nodurilor sau varfurilor graficului G, iar U, multimea muchiilor.
O muchie uÎU este deci o submultime {x,y} de varfuri distincte din X si se noteaza u=[x,y]. Vom spune despre varfurile x si y ca sunt adiacente in G iar despre u si x ca sunt incidente la fel ca si u si y. Se mai spune ca x si y sunt extremitatile muchiei u.
Daca u1 si u2 sunt doua muchii care au o extremitate comuna, ele vor fi numite de asemenea incidente.
Un graf poate fi reprezentat cu ajutorul unei figuri plane in care fiecarui varf i se asociaza un punct si fiecarei muchii [x,y], o linie curba care uneste in plan punctele ce corespund varfurilor x si y.
Inca un aspect interesant ar fi dezvoltarea naturala a teoriei grafurilor; de indata ce definitia unui graf a fost prezentata, notiunile si rezultatele par sa se nasca singure si in mod spontan, astfel incat cel care studiaza acest domeniu pare sa aiba impresia ca ar fi putut fi chiar el insusi creatorul acestui domeniu.
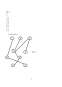
Exemplu: Fie G=(X,U) astfel incat X={1,2,3,4,5,6,7,8,9,10}, iar U={[1,5],[3,7],[4,6],[9,8],[10,2],[1,2],[9,4],[1,10],[6,8]}.
DEFINITIE: Un graf partial al grafului G=(X,U) este un graf G1=(X,V) astfel incat VÍU, adica G1 are aceeasi multime de varfuri ca G iar multimae de muchii V este chiar U sau o submultime a acesteia.
Exemplu: Pentru graficul G de mai sus, G1 = (X,V), unde V={[1,5],[2,10],[6,4]} este un graf partial.
Fig. 2
DEFINITIE: Un subgraf al unui graf G=(X,U) este un graf H=(Y,U) astfel incat YÌX iar V contine toate muchiile din U care au ambele extremitati in Y. Vom spune ca subgraful H este indus de multimea de varfuri Y.
Exemplu: Pentru graful din figura 1, daca Y={1,2,3,7,10} si V={[1,2],[1,10],[2,10],[3,7]}, atunci H=(Y,V) este subgraf al grafului G, subgraf reprezentat in figura 3.
Preview document
Conținut arhivă zip
- Grafuri Neorientate.DOC